Moment-Release

Member Release Derivation

Member-releases are the elimination of stiffness contributions at some degree of freedom. The most common is moment-release. Shear and axial-releases are also possible but not as common. Moment-release can be thought of as a pin connections, whereas shear and axial-release can be thought of as slotted connections.

Getting rid of stiffness contribution in a specific degree of freedom is not as simple as setting some terms within the stiffness matrix to zero. When one end is pinned, both force distribution and stiffness changes. Recall the stiffness matrix of a non-released member:

Let:

• DOF1 = i node shear
• DOF2 = i node moment
• DOF3 = j node shear
• DOF4 = j node moment
• FV, FM = fixed-end forces due to body load, temperature effect, pre-stress, or support settlement

To start, we expand the stiffness matrix into a system of equations:

Let’s say we have a hinge at the beginning node, because moment is released, M₂ should be 0. Sub in M₂=0 and isolate \(\theta_2\):

Therefore, the displacement of the released DOF is no longer linearly independent and require solving for \(\theta_4\) first. Next substitute the \(\theta_2\) expression into the four other expressions above. After a massive amount of algebra, and conversion to matrix form, we get our desired stiffness matrix.

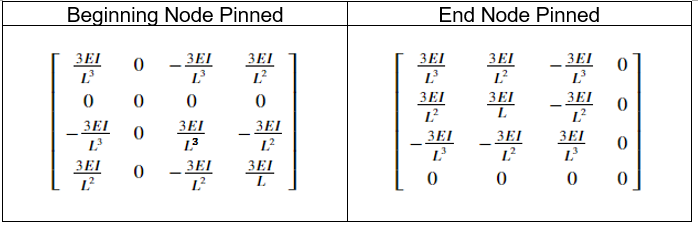
Notice how if the beginning node is pinned, then terms within row/column 2 (corresponding to DOF 2) of the matrix are set to 0. Similarly, if end node is pinned, then row/column 4 terms are set to 0. If both ends are pinned, then the member effectively becomes a truss element capable of only contributing axial stiffness.

Also notice how the fix-end force vectors are altered as well. Here is the python code if you want to try yourself:

# Imports
import sympy as sy
import numpy as np
A,I,L,J,G,E,x= sy.symbols('A,I,L,J,G,E,x')

# stiffness without shear deformation
d33 = sy.integrate((L-x)**2/E/I,[x,0,L])
d44 = sy.integrate(1/E/I,[x,0,L])
d34 = sy.integrate((L-x)/E/I,[x,0,L])
d43 = d34 #maxwell betti reciprocal theorem
d_noshear = sy.Matrix([
    [d33,d34],
    [d43,d44]])
T=sy.Matrix([
    [-1,-L,1,0],
    [0,-1,0,1]])
K_noshear = T.transpose() * d_noshear.inv() * T

# stiffness with shear deformation
d33 = sy.integrate((L-x)**2/E/I,[x,0,L]) + sy.integrate(1/G/A,[x,0,L]) 
d44 = sy.integrate(1/E/I,[x,0,L])
d34 = sy.integrate((L-x)/E/I,[x,0,L])
d43 = d34
d_shear = sy.Matrix([
    [d33,d34],
    [d43,d44]])
T=sy.Matrix([
    [-1,-L,1,0],
    [0,-1,0,1]])
K_shear = T.transpose() * d_shear.inv() * T

# Algebra with Sympy.
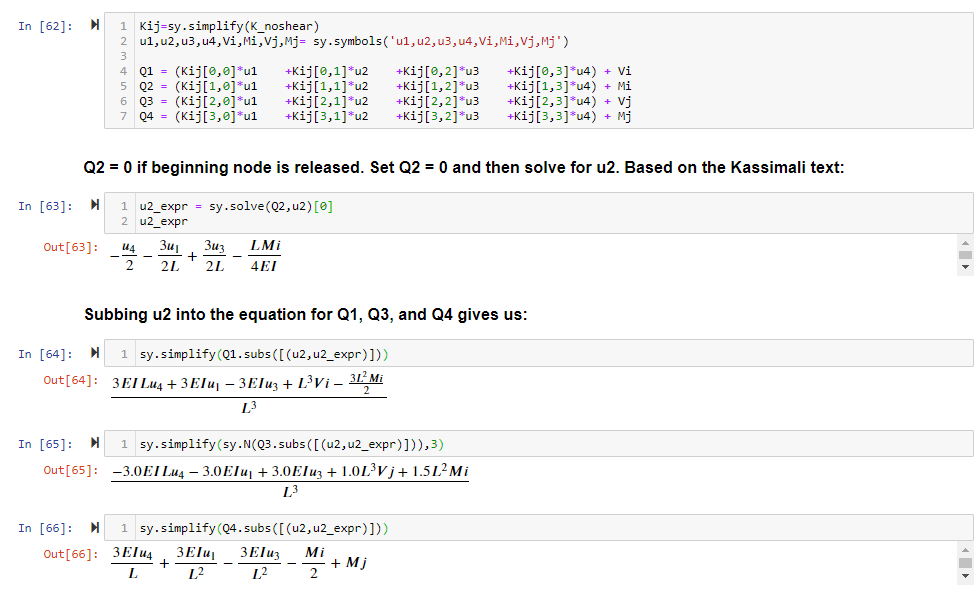
Kij=sy.simplify(K_noshear)
u1,u2,u3,u4,Vi,Mi,Vj,Mj= sy.symbols('u1,u2,u3,u4,Vi,Mi,Vj,Mj')

Q1 = (Kij[0,0]*u1    +Kij[0,1]*u2    +Kij[0,2]*u3    +Kij[0,3]*u4) + Vi
Q2 = (Kij[1,0]*u1    +Kij[1,1]*u2    +Kij[1,2]*u3    +Kij[1,3]*u4) + Mi
Q3 = (Kij[2,0]*u1    +Kij[2,1]*u2    +Kij[2,2]*u3    +Kij[2,3]*u4) + Vj
Q4 = (Kij[3,0]*u1    +Kij[3,1]*u2    +Kij[3,2]*u3    +Kij[3,3]*u4) + Mj

u2_expr = sy.solve(Q2,u2)[0]
sy.simplify(Q1.subs([(u2,u2_expr)]))
sy.simplify(sy.N(Q3.subs([(u2,u2_expr)])),3)
sy.simplify(Q4.subs([(u2,u2_expr)]))

Moment Release With Shear Deformation

What about shear deformation? Let’s use the same brute-force algebraic manipulation procedure above on the stiffness matrix with shear deformation. It gets really messy. Thankfully we have the magic that is Sympy symbolic math module.

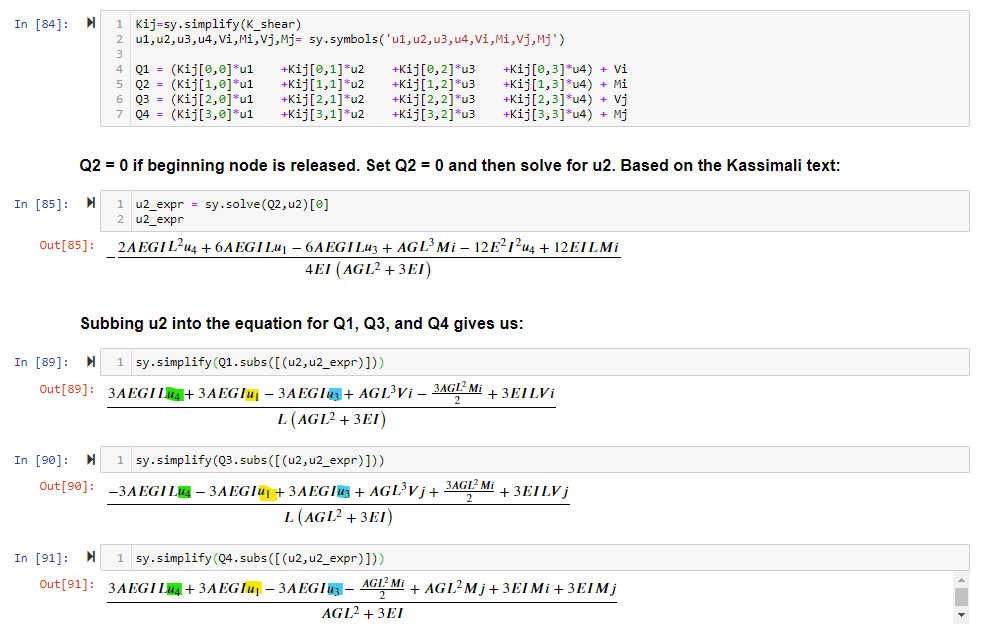
This was a pain to write down but here it is. Pin-fixed Beam stiffness matrix with shear deformation: